Arduino Pressure Sensor Tutorial | MPS20N0040D

This site has built up several tutorials on how to measure almost anything. Now, we add to that list an Arduino pressure sensor featuring the MPS20N0040D and the HX710B Analog-to-Digital IC.

In a Rush: Wiring the Pressure Sensor to Arduino

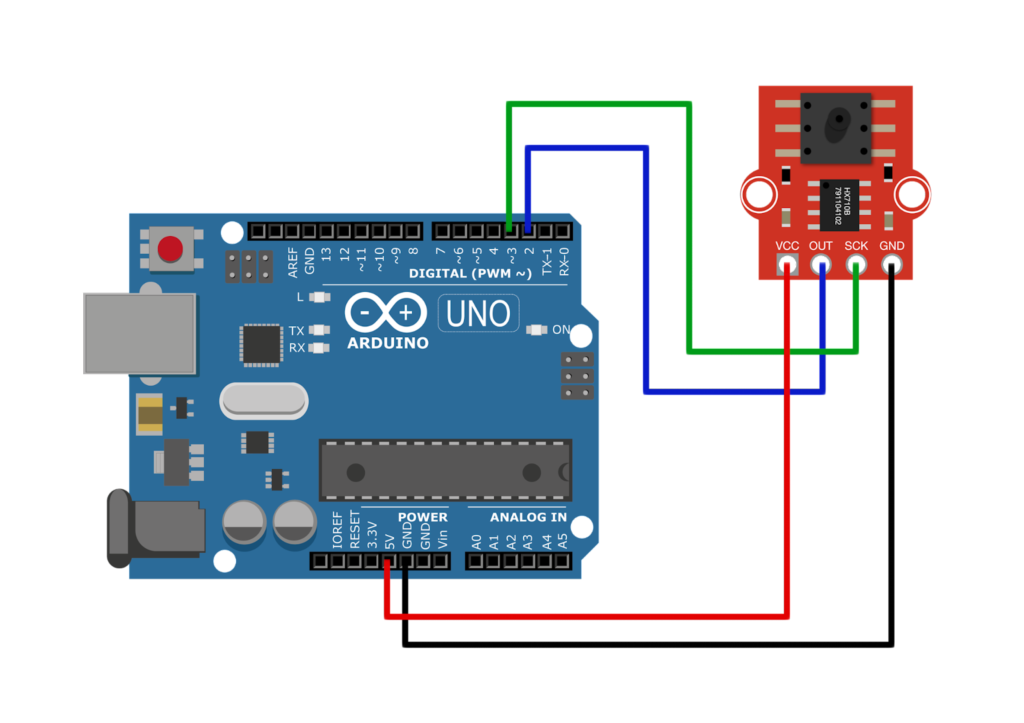
The pressure sensor conveniently sends out pulses according to the pressure data it reads. A clock pin provides timing for that data, like other synchronous protocols. Note that you can use any Arduino digital pin for the clock and data pins. Moreover, the Arduino’s 5V is enough to power the sensor module:

No library specific for this pressure sensor exists but you can use the same HX711 library for weight sensors. The HX711 and HX710B are both 24-bit analog-to-digital converters and provide the same pulse outputs. However, the original HX711 library gives out raw ADC values, not pressure. Hence, I decided to create my library that gives the output in Pascals, mmHg, atm, and psi.

You can clone/download the library on this page and place it directly in the Documents/Arduino/libraries folder.

Here’s an example sketch that displays the pressure in pascals in Serial Monitor:

#include "HX710B.h"

const int DOUT = 2;   //sensor data pin
const int SCLK  = 3;   //sensor clock pin

HX710B pressure_sensor; 

void setup() {
  Serial.begin(57600);
  pressure_sensor.begin(DOUT, SCLK);
}

void loop() {

  if (pressure_sensor.is_ready()) {
    Serial.print("Pascal: ");
    Serial.println(pressure_sensor.pascal());
    Serial.print("ATM: ");
    Serial.println(pressure_sensor.atm());
    Serial.print("mmHg: ");
    Serial.println(pressure_sensor.mmHg());
    Serial.print("PSI: ");
    Serial.println(pressure_sensor.psi());
  } else {
    Serial.println("Pressure sensor not found.");
  }

  delay(1000);
  
}

Want to learn more about how the pressure sensor works? Read on below.

In-Depth: How the MPS20N0040D Pressure Sensor Works

The MPS20N0040D measures the air or liquid pressure in its opening.

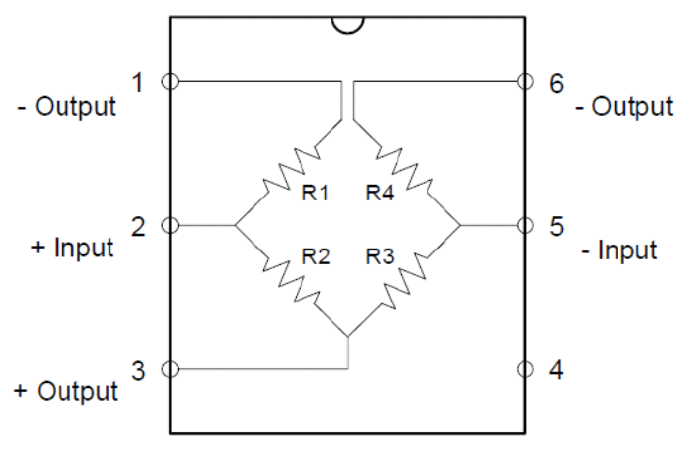
Bridge Circuit

The MPS20N0040D pressure sensor is a bridge circuit where one of the bridge elements is a pressure-sensitive resistor.  A source voltage is applied to the bridge at points 2 and 5 and output is measured at points 1 or 6, and 4.

The voltage output at points 1 or 6 and 4 is calculated using this formula:

You’ll notice that when all resistor values are equal, V_out is zero. A bridge with all resistor values equal is known as a balanced bridge.

Let’s say each resistor in the bridge is 10 ohms. Then the voltage output, for a 5V input, is:

When pressure is applied, one of the resistances in the bridge changes value. This unbalances the bridge and V_out is no longer zero.

Let’s say that because of the pressure, R1 changed from 20 ohms to 10 ohms. The value V_out then becomes

A 10-ohm change is a bit generous; in reality, the change in resistance is often very small. This corresponds to the voltage from the sensor Vout also being very small, way below the sensitivity of the Arduino’s ADC. Hence, there’s a need to use an external ADC, with a higher resolution than the Arduino’s 10-bit ADC. That’s the job of the HX710B.

Converting Voltage to Pressure

The HX710B is a 24-bit ADC that sends out pulses based on the voltage it reads. The higher the number of pulses within a specified frame, the higher the voltage measured. A 24-bit ADC can detect a voltage level as low as:

In comparison, a 10-bit ADC, the Arduino’s ADC via the analog input, can detect:

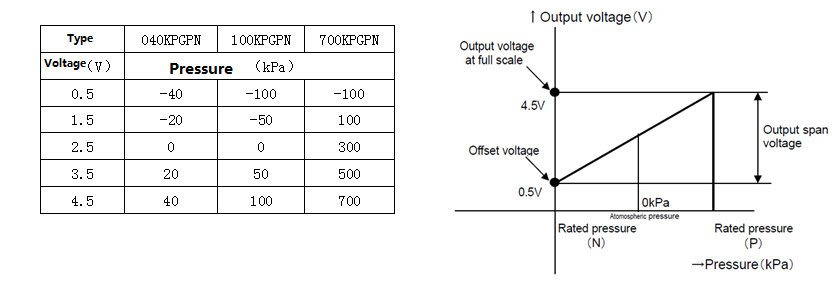
The MPS20N0040D gives out a voltage output that is linearly proportional to the applied pressure in kilopascals.

We can use this formula to convert the ADC output value to pressure in kilopascals.

For a 24-bit ADC like the HX710B, the equation becomes:

This is the equation used in the library to read the pressure in pascals.

For other units of pressure, we just use conversion factors:

Example Project: Liquid Level Sensor

It is possible for a pressure sensor to measure the current level of any liquid. Here's an example setup, where the KP610 device can be the MPS20N0040D pressure sensor (image from pressure-sensors.eu):

As the liquid level rises, the pressure inside the tube on the sensor increases. The height of the liquid is proportional to pressure with the formula:

where ρ is the density of the liquid, h is the liquid height and g is the acceleration due to gravity.